「新」动计划 · 编程入门 题面与答案解释
 2025-04-20  /articles/Primers-list/ 99+   27 分钟   4.0 k0次访问

「新」动计划 · 编程入门 题面与答案解释

欢迎前往我的仓库支持！

说明

本目录中的 Solutions.py 中存储了全部 LeetCode 「新」动计划 · 编程入门 的解法，为了方便阅读全部写进了一个类中，并附上了题号和题面描述的 URL，因此下文如无必要就不会粘贴题面。其中两道特别的题 #8 和 #9 使用的是 MySQL 语句完成的，因此另开一个 Markdown 文件 Solutions.MySQL.md 用于存储答案。

下面是对 20 道题目的理解和答案解释。

答案展示与思路解析

1
class Solutions():

1 LeetCode2235-两整数相加

1
2
def sum(self, num1: int, num2: int) -> int:
    return num1+num2

不必多言。

时间复杂度： O(1)

空间复杂度： O(1)

2 LeetCode2469-温度转换

1
2
def convertTemperature(self, celsius: float) -> list[float]:
    return [celsius+273.15,celsius*1.8+32]

只需要根据温度换算公式输出即可。

时间复杂度： O(1)

空间复杂度： O(1)

3 LeetCode2413-最小偶倍数

1
2
def smallestEvenMultiple(self, n: int) -> int:
    return n if n % 2 == 0 else n*2

通过数学方法解决：

  • 如果这个整数是偶数，直接输出即可。
  • 如果这个整数是奇数，输出它与 2 的积。（即：任意一个奇数总与 2 互质）

时间复杂度： O(1)

空间复杂度： O(1)

4 LeetCode2236-判断根结点是否等于子结点之和

这之前需要定义一个答案中用到的二叉树：

1
2
3
4
5
6
7
8
9
10
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
# 题目给出了一个数组 `root`，因此就有：
tree = TreeNode(root[0])
tree.left = TreeNode(root[1])
tree.right = TreeNode(root[2])

这样：

1
2
def checkTree(self, root: Optional[TreeNode]) -> bool:
	return True if root.left.val + root.right.val == root.val else False

容易发现只要一个简单的条件判断即可得到答案。

时间复杂度： O(1)

空间复杂度： O(1)

5 LeetCode1486-数组异或操作

1
2
3
4
5
def xorOperation(self, n: int, start: int) -> int:
    ans = 0
    for i in range(n):
        ans ^= start+2*i
    return ans

题目告诉我们 start + 2*1 就是num[i]，只要遍历一次即可得到答案。

（其中 ^ 是位运算的异或运算符）

时间复杂度： O(n)，n 是整型 n 。

空间复杂度： O(1)

6 LeetCode1512-好数对的数目

解法 Ⅰ

1
2
3
4
5
6
7
8
9
def numIdenticalPairs_1(self, nums: list[int]) -> int: 
    # 解法一
    # 采用了两层 for 循环，是一种暴力解法
    ans = 0
    for i in range(len(nums)):
        for j in range(len(nums)):
            if nums[i] == nums[j] and i<j:
                ans += 1
    return ans

类比 LeetCode1-两数之和，容易发现二者的思想其实是一样的。LeetCode1 是给出一个数组要求这个数组里找出两个数，使它们的和等于给定值；本题是使得数组中两个数相等。

所以我们首先考虑迭代两次，当 (i,j) 满足 nums[i] == nums[j] 且 i < j 时计数器（即解法一中的 ans）加一。这种方法必定出现最坏情况，即遍历列表 nums 次数为 len(nums) 的平方。

时间复杂度： O(n2)，n 是列表 nums 的长度。

空间复杂度： O(1)

解法 Ⅱ

1
2
3
4
5
6
7
8
9
10
11
12
def numIdenticalPairs_2(self, nums: list[int]) -> int:
    # 解法二
    # 使用字典减少了匹配次数
    d = dict()
    ans = 0
    for num in nums:
        if num in d:
            ans += d[num]
            d[num] += 1
        else:
            d[num] = 1
     return ans

同上。我们发现解法 Ⅰ 非常容易超时，于是我们设想类比 LeetCode1-两数之和看看能不能用 Python 的字典解决这个问题。

我们发现，针对题目中给出的有序整数对 (i,j) 总有 nums[i] == nums[j]，于是，我们可以创建形如

1
d = {key:value} # key 为 nums 中的整数 num，value 为 num 出现的次数

的字典。如果这个数在 nums 中第一次出现，就把它作为键并将它对应的值设置为 1。如果是第 n（n > 1）次出现，计数器就加上 n-1。这样，只需要遍历 nums 一次，就得到了答案。

Q：为什么加上 n-1 ？

A：根据计数原理，我们假设一张纸上有 n （n>2）个点，其中任意三个点都不在同一条直线上。我们发现，它们可以连成 1+2+3+…+(n-1) 条线段，也就是 $\frac{n(n-1)}{2}$ 条线段。

接着，我们增加一个点，这个点遵循上面的规则，于是线段条数增加 n 条（因为先前的 n 个点都要同这个新的点连结），以此类推。

把这个连线的过程回放到算法中，我们发现，如果把 nums 中的每个相同的数都看作一个点，那这些点连线的条数之和就是我们要的结果。同时因为两点只确定一条线段，就避免了判断 i 与 j 的大小。

时间复杂度： O(n)，n 是列表 nums 的长度。

空间复杂度： O(n)，最坏情况下需要存储 nums 中全部的整型。

7 LeetCode1534-统计好三元组

解法 Ⅰ

1
2
3
4
5
6
7
8
9
10
11
def countGoodTriplets_1(self, arr: list[int], a: int, b: int, c: int) -> int:
    # 解法一
    # 三层 for 循环，极其暴力，极其不优雅
    n = len(arr)
    ans = 0
    for i in range(n):
        for j in range(i+1,n):
            for k in range(j+1,n):
                if abs(arr[i] - arr[j]) <= a and abs(arr[j] - arr[k]) <= b and abs(arr[i] - arr[k]) <= c:
                    ans += 1
    return ans

注释已经写得很明确了。还好这道题限制了 arr 的长度3 <= arr.length <= 100，否则必定超时。

时间复杂度： O(n3)，n 是列表 arr 的长度。

空间复杂度： O(1)

解法 Ⅱ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def countGoodTriplets_2(self, arr: list[int], a: int, b: int, c: int) -> int:
    # 解法二
    # 这个解法很帅气，但我读不懂
    idx = sorted(range(len(arr)), key=lambda i: arr[i])
    ans = 0
    for j in idx:
        y = arr[j]
        left = [arr[i] for i in idx if i < j and abs(arr[i] - y) <= a]
        right = [arr[k] for k in idx if k > j and abs(arr[k] - y) <= b]
        k1 = k2 = 0
        for x in left:
            while k2 < len(right) and right[k2] <= x + c:
                k2 += 1
            while k1 < len(right) and right[k1] < x - c:
                k1 += 1
            ans += k2 - k1
    return ans

这是来自灵茶山大佬的解法，思想就是分成两个有序数组后使用双指针查找。但是，时间复杂度也只是下降到了 O(n2)，非常可惜。

具体解读等我看懂了再同步更新。

时间复杂度： O(n2logn)，n 是列表 arr 的长度。

空间复杂度： O(1)

8 LeetCode584-寻找用户推荐人

1
2
3
4
SELECT name
FROM customer
WHERE referee_Id != 2
   OR referee_Id IS NULL

处理这道题只有两个难点。一是不知道 MySQL 怎么用，二是 NULL 并不能简单地用布尔值判断，而是应该使用 MySQL 提供的 IS NULL 或 IS NOT NULL 运算。

第二点不能用布尔值的原因是，MySQL 是操作数据库的语言，是与现实紧密联系的。如果值是 NULL 自然只能认为不知道这个值，而不是用简单的 TRUE 或 FALSE 判断。

9 LeetCode1757-可回收且低脂的产品

1
2
3
4
SELECT product_id
FROM Products AS pr
WHERE pr.low_fats = 'Y' 
  AND pr.recyclable = 'Y';

同 8，只要会 MySQL 语句就很简单。格式问题不在这里赘述。

10 LeetCode709-转换成小写字母

解法 Ⅰ

1
2
3
4
def toLowerCase_1(self, s: str) -> str:
    # 解法一
    # 直接调用 Python 内置函数
    return s.lower()

不必多言。

时间复杂度： O(n)，n 是字符串 str 的长度。

空间复杂度： O(1)

解法Ⅱ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def toLowerCase_2(self, s: str) -> str:
    # 解法二
    # 假设 Python 没有提供 str.lower() 这样方便的函数，就需要通过 ASCII 转小写
    return "".join(chr(ochar | 32) if 65 <= (ochar := ord(char)) <= 90 else char for char in s)
    # 为了方便理解，下面是展开式。其中提到的变量 ans 并不是必要的
    #     ans = []
    #     for char in s:
    #         ochar = ord(char)  # 计算字符的 ASCII 值
    #         if 65 <= ochar <= 90:
    #             lower_char = chr(ochar | 32)
    #             ans.append(lower_char)
    #         else:
    #             ans.append(char)
    #     return "".join(ans)

在 ASCII 中，大写英文字母占用 6590，小写字母占用 97122，中间间隔 32。

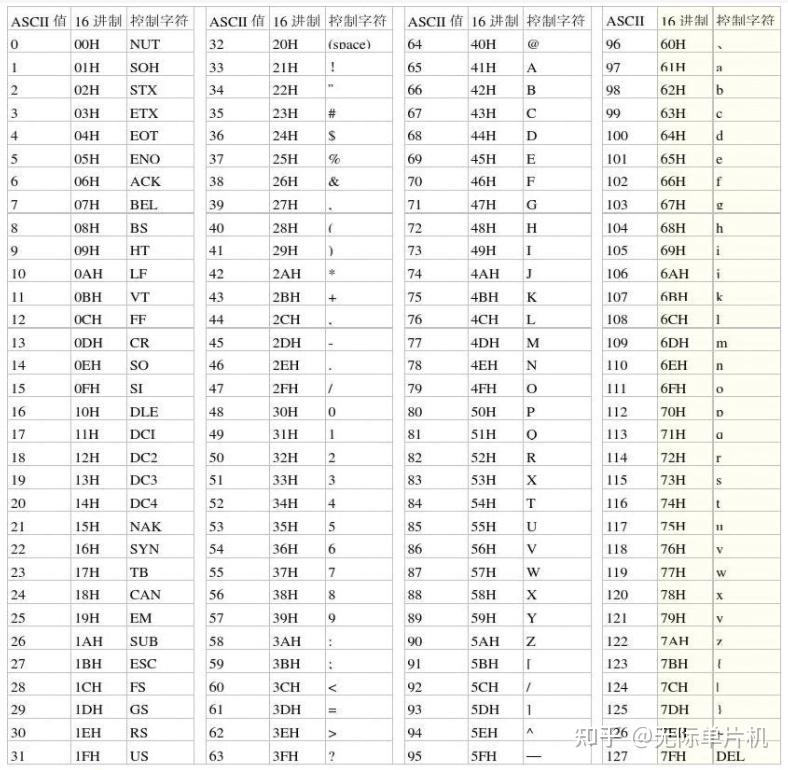
ASCII 表

时间复杂度： O(n)，n 是字符串 str 的长度。

空间复杂度： O(1)

11 LeetCode258-各位相加

1
2
def addDigits(self, num: int) -> int:
    return (num-1)%9+1 if num >= 1 else 0

我们在小学的时候就学习过怎样快速判断一个正整数是不是 3 的倍数。方法就是将待判断的数的每一位都加起来，得到一个新的数，如果这个新的数是 3 的倍数，那么这个待判断的数也是 3 的倍数。

这个过程与这道题的要求非常相似，于是我们设想：通过类比计算一个数是否是 3 的倍数，得到这个算法。

当然，如果根据上述，我们会发现得到的结果永远小于 3，因此我们借助 10 以下同时也是 3 的倍数 9 来辅助处理这个问题。这样的话，得到的结果就限定在了 [0,8]，如何处理结果为 9 我们后面再说。

让我们先做一个实验：

假设 num = 102734，那么：

1+0+2+7+3+4 == 19, 1+7 == 8

107234%9 == 8

非常符合我们的猜想。不失一般性，我们将这个结论推广到 $[0,2^{31}-1]$ 这个区间内。（证明过程请自行查找关键词“数根”，这里不赘述）

但是我们容易发现：一旦 num 是 9 的正整数倍，结果就会变为零，这明显不是我们想要的。于是我们对 num 进行偏移，这样就能保证当 num 是 9 的正整数倍时结果不为零。

因为 num 必定是自然数，因此选择 num-1。这样，num-1 模 9 取余得到的结果就变成 num 同样操作后减去一（当然，上面提到的情况除外），我们再把它加上。

还有最后一个例外：0。对 0 做一个简单的条件判断即可。

时间复杂度： O(1)

空间复杂度： O(1)

12 LeetCode1281-整数中的各位积和之差

1
2
3
4
5
6
def subtractProductAndSum(self, n: int) -> int:
    prod, SUM = 1, 0 
    for num in str(n):
        prod *= int(num)
        SUM += int(num)
    return prod-SUM

无需多言。顺次获取每一位数

时间复杂度： O(logn)，其中 n 是整型 n 变为字符串后的长度。显然只有整型 n 的位数（而不是数的大小）增加时字符串 n 长度才增加，它们满足对数增长关系。

空间复杂度： O(1)

13 LeetCode231-2的幂

1
2
def isPowerOfTwo(self, n):
    return n > 0 and n & (n - 1) == 0

我们知道 2 的幂一定是正数，因此我们得到第一个条件：n>0

同时我们经过观察，发现：当一个十进制数 n 是 2 的正整数次幂时，n 对应的二进制必定首位是 1，其余位全是 0，且 n-1 的首位是零，其余位全是 1。这意味着我们只需要采用位运算和，就能得出答案。

时间复杂度： O(1)

空间复杂度： O(1)

14 LeetCode326-3的幂

1
2
def isPowerOfThree(self, n: int) -> bool:
    return True if n > 0 and 1162261467 % n == 0 else False

这道题……我得承认我没有好的想法，只是把数据范围区间内 3 的幂的最大值（1162261467）预先求出来，再把这个数除以 n，如果余数是 0 那 n 自然是 3 的正整数次幂。

这个思路完全可以套到13 LeetCode231-2的幂中，但是太不优雅就没有写出来。

时间复杂度： O(1)

空间复杂度： O(1)

15 LeetCode263-丑数

1
2
3
4
5
6
7
8
9
10
11
def isUgly(self, n: int) -> bool:
    if n <= 0:
        return False
    else:
        while n % 3 == 0:
            n /= 3
        while n % 5 == 0:
            n /= 5
        while n % 2 == 0:
            n /= 2
        return n == 1

丑数是个已经被承认的数学概念，除了暴力也没有别的好方法。

时间复杂度： O(logn)，其中 n 是整型 n。取对数增长的原因是，每一次做除法，n都会变到原来的 1/m，其中 m 是 2 或 3 或 5，n 减小的速度会越来越慢，直到得出结果。因此可以认为时间复杂度是 O(logn)。

空间复杂度： O(1)

16 LeetCode1470-重新排列数组

1
2
3
4
5
6
7
def shuffle(self, nums: list[int], n: int) -> list[int]:
    ans = list()
    for i in range(n):
        ans.append(nums[i])
        ans.append(nums[n])
        n += 1
    return ans

容易发现，len(nums) 必是偶数，因此我们用两个指针 i 和 n 来实现功能

假如我们把 nums 等分成两半，就能发现 num[n] 恰好是紧靠中线右侧的一项，也就是题目要求的 y1，按照这个思路，每循环一次 i 与 n 都加一，就能得到答案。

时间复杂度： O(n)，n 是 nums 的长度。

空间复杂度： O(1)

17 LeetCode867-转置矩阵

1
2
3
4
5
6
7
def transpose(self, matrix: list[list[int]]) -> list[list[int]]:
    i, j = len(matrix), len(matrix[0])
    ans = [[0] * i for num in range(j)]
    for m in range(i):
        for n in range(j):
            ans[n][m] = matrix[m][n]
    return ans

思路就是创建一个行列数与 matrix 相反的二维列表，再一个个填进去。

时间复杂度： O(n2)，n 是 matrix 行数与列数中的较高项。

空间复杂度： O(1)

18 LeetCode1422-分割字符串的最大得分

1
2
3
4
5
6
7
8
9
10
def maxScore(self, s: str) -> int:
    r = s.count("1") # 右计数器
    l = ans = 0 # 左计数器和答案
    for i in s[:-1]:
        if i == "0":
            l += 1
        else:
            r -= 1
        ans = max(ans,l+r)
    return ans

题目中把 s 分割成了长度均不为零的两部分，计算左侧 0 的数目与右侧 1 的数目之和（称作“得分”）的最大值。

容易想到，遍历字符串一次（把这个称作分界线）。如果分界线遍历到的是 0，左计数器就加 1；如果是 1，右计数器就减 1。

当然，在这之前，假设全部字符串都被归到右边，那得分就是 s 中 1 的数目，把它作为右计数器的起始值。

还有最后一个坑，由于分割后的字符串必定不是空字符串，给 s 切片时就需要防止分界线抵达最后一位。因为分割字符串时分割的点必定在分界线与下一位之间。

时间复杂度： O(n)，n 是字符串的长度。

空间复杂度： O(1)

19 LeetCode2586-统计范围内的元音字符串数

1
2
3
4
5
6
7
def vowelStrings(self, words: List[str], left: int, right: int) -> int:
    ans = 0
    vowels = "aeiou"
    for i in range(left,right+1):
        if words[i][0] in vowels and words[i][-1] in vowels:
            ans += 1
    return ans

一道挺有趣的题，只要遍历 words 中在[left, right]这个区间中的词并且判断首尾就行了。

时间复杂度： O(n)，n 是需要遍历的词数。

空间复杂度： O(1)，仅占用一个长度恒为 5 的字符串。

20 LeetCode852-山脉数组的峰顶索引

1
2
3
4
5
6
7
8
9
def peakIndexInMountainArray(self, arr: List[int]) -> int:
    l, r = 0, len(arr)-1
    while l<r:
        m = l + (r - l) // 2
        if arr[m] < arr[m+1]:
            l = m + 1
        else:
            r = m
    return l

这道题与前面 19 题有一个最大的区别（不是难度！），就是它限制了时间复杂度为 O(logn)。

一般地，针对这种限制时间复杂度的题，我的建议是在互联网搜索“时间复杂度为 xxx 的经典算法”，然后根据实际情况修改。例如，既然时间复杂度是 O(logn)，很快就能检索到二分查找。

然后，又因为我们要找的数必定是既大于它左边又大于它右边的，我们就有了搜索方向，二分查找成立。

把左右指针设置为 0 和末尾，反复取半。容易发现，每取一半，将用到的时间就又少一点，这满足题目要求的 O(logn)。注意避免死循环和溢出，当 l == r 时就可以返回答案了。

时间复杂度： O(logn)，其中 n 是 arr 的长度。

空间复杂度： O(1)

结语

这整一套题单我花了一天多一点，断断续续做完的，感觉设计的很不错，非常适合像我这样的初学者。我觉得自己已经深深地学习了。

下一道题就等下一个周末再更新吧，See ya~

(The end)

「新」动计划 · 编程入门 题面与答案解释

https://karlbaey.top/articles/Primers-list/

发布于

2025-04-20

更新于

2025-04-20

许可协议

# 推荐文章
  1.十年边缘//The Edge of a Decade

喜欢这篇文章？打赏一下作者吧

评论
关注我

:D 一言句子获取中...

最新文章

分类

归档

标签

Delights7
GettingStarted7
GitHub4
Guide4
DailyLife3
Milestone3
Reviews3
Algos2
LeetCode2
Markdown2
Past2
Python2
Desktop1
Feed1
Files1
Lanzou1
Minecraft1
Music1
Original1
Sadness1
查看全部>>

订阅更新

这是我的正式 feed（中国大陆地区无法访问）

follow.it

在这里输入你的邮箱并确认，就能收到我的博客更新通知了！

×