卡尔白算法之路的开山之作：LeetCode20-有效的括号

欢迎前往我的仓库支持！

题面描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：
    I: s = "()"
    O: True

示例 2：
    I: s = "()[]{}"
    O: True

示例 3：
    I: s = "([)]"
    O: False

示例 4：
    I: s = "(]"
    O: False

示例 5：
    I: s = "([{}])"
    O: True
    
其中 1 =< s.length =< 10^4

解法与逻辑关系的解释

这是我的解法：

class Solution:
    def isValid(self,s: str) -> bool:
        brackets = {")":"(","]":"[","}":"{"}
        chars = list()
        for char in s:
            if char in brackets: # 优先处理右括号
                if not chars or chars[-1] != brackets[char]: # 栈为空 / 栈末位与待检测括号不匹配
                    return False
                chars.pop()
            else: # 处理左括号
                chars.append(char) # 直接压入栈
        return not chars # 处理完毕，栈为空则 s 有效

变量名解释：

s： 待检测括号。

chars：空栈，存储单个括号用。

char：s 中每一个括号。

brackets：存储右-左括号的键-值对的字典。

算法的要求很简单：每个左括号一定能在它右侧的某一位置找到与它对应的右括号**（反之亦然），此时称它与它的右括号为一对有效的括号**，并且它的右括号不会穿插在另一对有效的括号中。

这意味着我需要使用栈，遵循后进先出原则（Last In First Out），以便于在右括号与它的左括号匹配上时能够及时地将这一对有效的括号弹出，不影响后续的判断。所以用到 Python 的字典建立映射关系。

我的困惑是第 7 行代码

if not chars or chars[-1] != brackets[char]:

不过在这之前还要检查第 6 行：if char in brackets:。Python 的字典在使用 in 运算符时只检查键而不是值，也就是说，brackets 中的全部键均是右括号，只要第 6 行的代码能够判断待检测括号是右括号即可。

or 把前后分成两个条件，也就是 not chars 和 chars[-1] != brackets[char]：

1. not chars：当 chars 为空时，这个条件的结果是 True。栈为空还有右括号未匹配自然无效。
2. chars[-1] != brackets[char]：brackets[char]是这个右括号的对应左括号，此时它的左侧（也就是栈的末端）并不是它对应的左括号，说明这对括号无效。

这里的关系理顺了，下面直接把左括号压入栈的做法也就很好理解了。

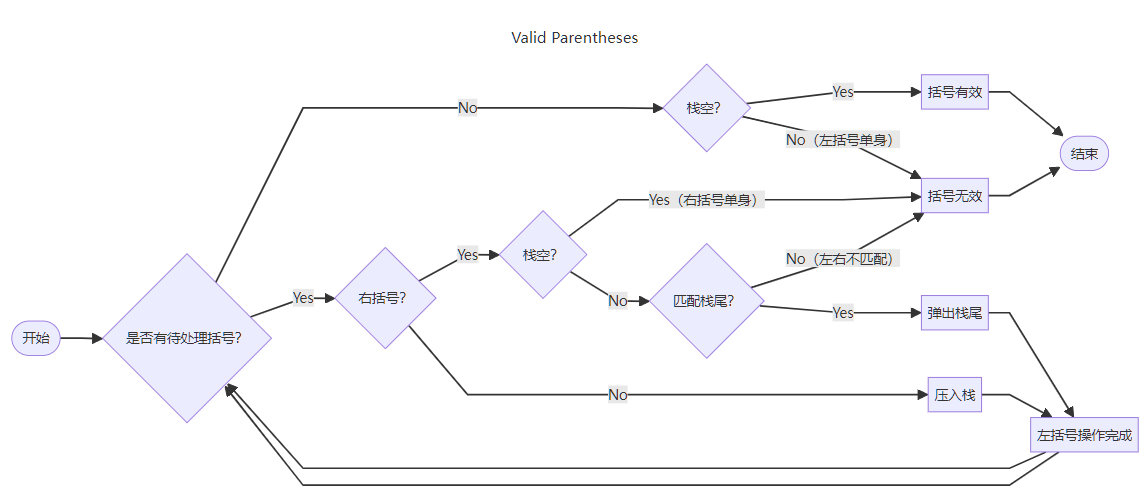
流程图演示

时间/空间复杂度

时间复杂度： O(n)

• 代码遍历整个字符串一次，每个字符处理时间为 O(1)。字典查找、列表的末尾插入（append）和删除（pop）操作均为常数时间复杂度。

空间复杂度： O(n)

• 最坏情况下（如所有字符均为左括号），chars 列表需要存储所有字符，占用 O(n) 空间。即使存在部分匹配，空间复杂度仍由输入字符串长度决定。