复杂度是能够用来衡量程序好坏的概念，它用来描述随着输入大小 n 的增长，程序的处理时间和占用空间会怎样改变。其中有一个观念不可忽略：就是我们通常假设 n 是一个比较大的数（例如 10,000），这样计算复杂度才是有价值的，否则，在 n 很小时，复杂度无法明确地展示程序的好坏。

复杂度的诞生

用一个比喻开始。

你是一名图书馆管理员。这天馆长找你，让你在一个有 100,000 本书的书架上找到所有的《三体2：黑暗森林》。

这个书架可能有两种最极端的情况。

• A：所有的书杂乱地放在书架上，毫无规律。
• B：所有的书都严格地按照书名拼音 A-Z 的顺序整齐摆好。

更有利于我们搜索的排列方式显然是 B。在后者的前提下，我们只要在书架找到“S”开头的书籍，接着找“T”……很有可能找了二十本不到，就找完需要的书了。

相反，对于 A，在最坏的前提下，需要找完所有 100,000 本书才能知道是否找完。

复杂度（complexity）就是为了衡量你这个“找书”任务的效率而诞生的。它不关心你的手速有多快（处理器主频），也不关心图书馆的灯光亮不亮（编程语言的速度），它只关心这个方法本身的好坏。我们需要一个统一的标准，来评判不同“找书方法”（算法）的效率，这就是时间复杂度和空间复杂度。

为什么不用实际时间？因为同一段代码在不同性能的电脑上运行，时间是不一样的。我们应该关注算法内在的、固有的效率。

今天的家用计算机每秒能执行几十亿次运算，而且不同计算机性能差异不可忽略，所以找一个标准来衡量程序好坏是很必要的。

复杂度的计算

时间复杂度

回到找书的例子。

我们如果需要知道一本书的书名，就需要拿起书本，看看封面。这个看封面的操作我们称作基本操作。

假设书架上有 n 本书：

• 在情况 A 里，我们需要拿起每一本书。这时需要执行 n 次基本操作。
• 在情况 B 里，我们可以使用二分查找。看看第 n/2 本的书名，如果发现首字母是 M，就往后半部分找，以此类推。每次要找的部分都是上一次的一半（也就是查找部分的大小从 n 开始，一直往后就是 n/2、n/4、n/8……），所以这样找书只需要 log_2 n 次基本操作。
  • 二分查找是一种搜索思路。这种搜索思路可以这样解释：将待搜索的部分平分，然后根据中点，确认当前要找的东西在哪一部分，再把这一部分继续平分。直到没有或只剩一个要搜索的部分，就得到答案了。

这里的 n 和 log_2 n 就是两种找书方案的复杂度。当 n 变得非常大时，我们也能大概看出这两种方案需要的基本操作次数。

但是放在写好的程序里，不需要非常精确地说明每一个程序的复杂度。因为常数（log_2 n 中的 2 就是常数）会在 n 变得非常大时变得不重要。我们只关心增长的趋势和速度。

所以计算机科学家借用了数学的渐进分析，使用大 O 表示法¹表示“大约”的复杂度等级。常见的等级有：

• O(1) - 常数时间： 这是最好的情况。就像我们手头有一个魔法口袋，无论图书馆有多少书（n 有多大），你伸手一次就能直接拿出《三体2》。操作次数不随 2 增大而改变。
  • 现实例子：通过数组下标直接访问元素 arr[5]。
• O(log n) - 对数时间： 非常高效！ 就像我们的有序图书馆，用二分法找书。N即使增长到原来的2倍，你只需要多找1次。书从100本变成100万本，你只需要从7次操作增加到20次操作。
  • 现实例子：二分查找。
• O(n) - 线性时间： 比如在乱序图书馆里一本一本地找。书的数量增加几倍，你需要的时间也大致增加几倍。这是最公平、最常见的情况。
  • 现实例子：遍历一个数组寻找最大值。
• O(n²) - 平方时间： 情况开始恶化。这就像馆长让你不是找一本书，而是给所有书都拍一张“合影”。你需要让每本书都和另一本配对。操作次数大约是 n*n 次。如果书从 100 本增加到 1,000 本，你的工作量会从 10,000 次暴增到 1,000,000 次！
  • 现实例子：使用双重循环检查数组中是否有重复元素。
• O(2ⁿ) - 指数时间： 这就像“汉诺塔”游戏，盘每增加一个，所需步骤就会翻倍。n 稍微大一点（比如超过 63），这个算法可能直到宇宙毁灭都算不完。这是我们拼命想要避免的复杂度。
  • 现实例子：一个非常低效的递归解法，比如暴力穷举所有组合。

下面这张图展示了不同时间复杂度的增长趋势。横轴表示输入数据量，纵轴表示消耗时间。

通常来说，一个遍历输入的 for 循环就会占用 O(n) 的时间复杂度，而两个循环嵌套就会占用 O(n²) 的时间复杂度，以此类推。上升趋势更大就会涉及到回溯算法和递归。

时间复杂度的计算遵循渐进分析，也就是只保留最高次项。例如，我们分析得到一个算法的时间复杂度是 O(n²) + O(n)。

func Aaaaaaa(inp []int) int {
    for i := range inp {
        for j := range inp { // 双层嵌套 -> O(n^2)
            // Something
        }
    }
    
    for k := range inp { // O(n)
        // Another something
    }
    
    return 0
}

它实际上的复杂度应该是 O(n²)，因为 O(n²) 的增速远大于 O(n)，O(n) 造成的影响在 n 很大时几乎可以忽略。

空间复杂度

空间复杂度直接反映了为了程序执行而额外占用的空间大小。

任务本身就需要一个图书馆（存储所有书），这个空间是固有的、无法优化的，输出值也是一样。

我们关心的是你作为管理员，在执行“找书”这个任务时，需要额外申请多少工具和空间。

同样用大O表示法：

• O(1)： 只需要固定大小的空间（比如几个变量），原地操作，非常省空间。比如找书时我们只用记住当前在手上的书，这就是常数空间。
• O(n)： 需要额外开辟一个和输入数据量 n 成正比的数组或列表。如果要把所有的书名都记在一个本子上，就相当于额外占用了一个大小为 n 的空间。
• O(n²)： 需要开辟一个二维数组（比如矩阵），空间消耗巨大。

对于一个递归深度为 n 的算法（计算阶乘就属于一种递归），其空间复杂度至少为 O(n)。因为每次递归调用，空间占用都会在原有基础上 +1。

通常，我们追求的是时间更快或空间更省的算法。但鱼和熊掌不可兼得，很多时候需要在时间和空间之间进行权衡：

• 有时我们可以用空间换时间：比如多建一个索引本（消耗额外空间），但能让以后找书的速度飞快（减少时间）。
• 有时我们可以用时间换空间：比如为了不占用新本子，我们宁愿在原始书堆里多花时间慢慢找。

具体代码

例如 LeetCode 209 长度最小的子数组，我们使用滑动窗口算法，就能在 O(n) 的时间复杂度以内解决。因为每个元素最多被窗口的左端和右端分别访问一次。

func minSubArrayLen(target int, nums []int) int {
    var now, l int
    var ans int = 100100 // 用一个不可能的大数初始化答案

    for r, num := range nums { // `r` 是窗口右边界，循环向右移动
        now += num
        for now >= target {
            ans = min(ans, r-l+1)
            now -= nums[l] // 当窗口满足条件时，尝试收缩左边界以找到更优解
            l++ // 左边界右移
        }
    }
    if ans == 100100 {
        return 0
    }
    return ans
}

这段代码的思路是这样的：

• 初始化 ans 和 now 作为辅助变量。
• now 窗口右端对应值 nums[r]，窗口右端扩张。
  • 如果 now >= target，那么以当前窗口长度 r-l+1 和 ans 中的较小值作为答案。
  • now 减去 nums[l]，窗口左端收缩
  • 如果此时仍然 now >= target，那么更新 ans；否则跳出循环，重新 now += nums[r]
• 最后排除无满足窗口的情况。

上面的代码虽然嵌套了两个 for 循环，但是因为这实际上是两个分开执行的循环，所以最极端的时间复杂度应该是 O(2n) 而不是 O(n²)。

由于我们只使用了几个整数用来存临时变量，所以空间复杂度是 O(1)

滑动窗口算法是双指针算法的变形，而且因为入门门槛低，我打算下一期就做这个了。

滑动窗口是很简单的，熟练之后可以在很短的时间里默写出来。

再看一个 O(log n) 的示例。

LeetCode 852. 山脉数组的峰顶索引：这道题最快的方式就是使用二分查找。我们只要判断中点右侧的值比中点值大还是小就能知道峰值方向。

func peakIndexInMountainArray(arr []int) int {
    var l, mid int
    r := len(arr) - 1
    
    for r > l {
        mid = (r + l) / 2 // 找中点
        if arr[mid] < arr[mid+1] { // 判断峰值方向
            l = mid + 1
        } else {
            r = mid
        }
    }
    return l
}

这样，l 和 r 就会迅速地朝峰值靠近，直到 l == r，我们就找到了峰值的索引。

因为每一次查找，数组 arr 都被分割成了原来的二分之一，也就是说，实际上只执行了 $\log_2{\textrm{n}}$ 次操作（n = len(arr)）。

我们知道，对数是指数的逆运算，因此对于方程

$$2^x = n$$

此处的 x 就是我们需要的操作次数。那么

$$x = \log_2{n}$$

转换成时间复杂度，二分查找的时间复杂度就是 O(log n)。

如果 n == 100000000，我们只需要 $\log_2{\textrm{n}} \approx 27$ 次操作。这是非常高效的。

二分查找的缺陷在于，如果边界（l 和 r）没有设置好，很容易超出索引或者导致溢出。

二分查找的空间复杂度是 O(1)，我们只用了若干个 int 类型变量。

额外部分

算法执行时间与输入规模 n 的关系称为时间复杂度，通常用 大 O 表示法 写成 T(n) = O(f(n))。这里的 O(f(n)) 并不意味着算法真的花费了 f(n) 的时间，而是表示其增长速率不会超过 f(n) 的常数倍，从而为我们提供了一个衡量算法效率的标尺。

也就是说，算法执行时间实际上受到 f(n)²的限制。

除了大 O 表示法，还有其他的符号能描述算法的好坏。

我们常用的通常有这三个符号：

• Ο：表示上界。描述的是算法运行时间最坏情况的表现。

• Ω：表示下界。描述的是算法运行时间最好情况的表现。

• Θ：既是上界也是下界，Θ 表示的是算法的运行时间有一个确定的增长级别。也就是说，如果某个算法的时间复杂度是Θ(f(n))，那么它的运行时间最终会被 c1 * f(n) 和 c2 * f(n) 限制在中间（其中c1、c2是常数）。它不是等于，而是增长速率与f(n)相同。

Ο 是渐进上界，Ω 是渐进下界。Θ 需同时满足大 Ο 和 Ω，所以称为确界。Ο 是复杂度分析中最常用的，因为它表示了最差效率。

中译中就是，Ο 告诉我们“算法再慢不会慢于这个程度”，Ω 告诉我们“算法再快不会快于这个程度”，而 Θ 则告诉我们“算法的速度基本就在这个范围内”。

例如，对于滑动窗口算法：

• 最好情况：Ω(1)（第一个元素就满足条件）
• 最坏情况：O(n)
• 平均情况：O(n)
• 它不能用Θ来描述，因为它的最好和最坏情况不在同一个增长级别上。

而对于快速排序：

• 最坏情况（例如数组已排序或逆序，这会导致分区严重不均衡）：O(n²)
• 最好情况（划分完全均衡）：Ω(n log n)。
• 平均情况： Θ(n log n)。
• 尽管存在最坏的 O(n²) 情况，但通过随机选取基准值，容易证明，快速排序的平均（期望）时间复杂度是 Θ(n log n)。³因为在随机化后，每一种分区虽然都有可能，但导致极差性能的划分情况出现的概率非常低，而导致良好性能的划分情况占据了主导，使得整体平均性能足够优秀。

对于时间复杂度分析，我们关心的是输入规模 n 趋于无穷大时的趋势，而非具体的执行时间。通过渐进分析，我们可以抽象掉硬件、常数项等细节，直接比较算法的本质效率。

可以通过下面这张图来比较复杂度的较大值，越靠右效率越差。

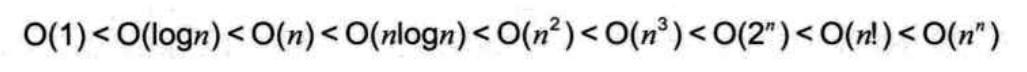
复杂度是用来衡量程序好坏的概念，分为时间复杂度和空间复杂度。时间复杂度能描述算法执行所需的大致时间，而空间复杂度描述算法运行时所需的内存空间。复杂度是用来评估算法效率的主要指标。一些算法因为复杂度表现非常优异，我们直到现在还在使用。例如二分查找（O(log n)），迪杰斯特拉最短路径算法（O(n²)）⁴。

下一期 #4 将会开始经典算法部分，第一期就是双指针以及它的变形。

🎉撒花🎉