程序设计#4%1【经典算法】双指针和滑动窗口·第二部分
上一期中,我们接触了双指针算法的两种基本用法:快慢指针和对撞指针。其中,快慢指针适用于解决去重问题以及解决有环的链表的问题;而对撞指针适合在排好序的数组中寻找元组(例如元组中每个数的和恰好是定值)。
我们提到,双指针算法就像是在漆黑的走廊里派出两名干员。现在我们把干员换成一盏大功率探照灯,它能够一次把走廊中的一部分照亮,原来的两名干员就变成了光照亮之处的左右端点。
有没有发现,这段被照亮的地方就好比在走廊中打开了一个窗口。所以,这种算法思想就叫做滑动窗口算法。
滑动窗口 - 长度固定
我们从简单的情况说起。
假设我们在大数组里寻找一个长度固定为 k 的子数组,并且让小数组元素的平均值最大,因为子数组长度固定,所以我们需要让子数组元素的和最大。
我们可以使用 now 来记录当前窗口内的和,ans 每次循环都与 now 比较取较大值。
ans = max(now, ans)这也就是 leco634 子数组最大平均数 I 的过程。
子数组 - 和最大/最小
leco643:
给你一个由
n个元素组成的整数数组nums和一个整数k。请你找出平均数最大且 长度为
k的连续子数组,并输出该最大平均数。任何误差小于 10-5 的答案都将被视为正确答案。
定长滑动窗口其实就是速度相同且同向而行的双指针,因此我们只要用快慢指针的思想改一改即可。在这个过程中我们需要在 now 加上每个窗口右端点(用 nums[r] 表示)的值,并且在窗口长度已经达到 k 时,减去窗口左端点的值(用 nums[l] 表示)。也就是说:
- 窗口右端进入(
now += nums[r]) - 判断
r >= ktrue:更新ans的值(ans = max(now, ans))false:什么也不做,进入下一次循环
now减去左端点的值nusm[l]
l == r-k+1的原因:数组中,从
nums[l]到nums[r]应该有k个元素。也就是说,从l开始数,数(k-1)个数就是r。如下所示。
l == r-(k-1) => l == r-k+1
⚠️注意:因为要求找的是数组中的最大平均值,所以必须把 ans 初始化为一个很小的数。把 ans 初始化为 0 的话,如果数组中的每个数都是负数,那就会出现返回值是 0 的错误(此时 ans 必然大于等于任何情况下的 now)。这是一个坑点,我自己就踩过好几次。
写成代码,如下所示。
func findMaxAverage(nums []int, k int) float64 {
var now int
var ans int = -2147483647 // 一个小到不可能的数
for r := range nums {
now += nums[r] // 一定要窗口右端先进!
l := r-k+1
if l < 0 { // 窗口长不足 k
continue
}
ans = max(ans, now) // 取最大值
now -= nums[l] // 左端出窗口
}
return float64(ans) / float64(k)
}当然了,对于字符串,我们也可以用类似的方案。例如 leco2379。
给你一个长度为
n下标从 0 开始的字符串blocks,blocks[i]要么是'W'要么是'B',表示第i块的颜色。字符'W'和'B'分别表示白色和黑色。给你一个整数
k,表示想要 连续 黑色块的数目。每一次操作中,你可以选择一个白色块将它 涂成 黑色块。
请你返回至少出现 一次 连续
k个黑色块的 最少 操作次数。
这道题实际上就是在问:一个长为 k 的子串中,'B' 的最大数目是多少? 也可以是问 'W' 的最小数目。
所以运用与上面类似的思路,就能得到如下的代码。
func minimumRecolors(blocks string, k int) int {
var now, ans int
for r := range blocks {
// 这里是求最多的黑色
// 如果换成 if blocks[r] == 'W' {} 那就是求最少的白色
if blocks[r] == 'B' {
now++
}
// 下方操作同 leco643
l := r-k+1
if l < 0 {
continue
}
ans = max(now, ans)
if blocks[l] == 'B' {
now--
}
}
return k-ans // 这里因为求到的是 B 的最大值,所以要用 k 去减
}我们能够从上面的过程推导出一个定长滑动窗口的标准流程。
- 进入窗口:右端点进入窗口,常常写作
now += nums[r]。 - 判断边界:因为我们已经知道,左端点
l实际上就是r-k+1,所以必须确保l >= 0(否则会超出索引),这样能确保窗口长度必定在等于k时才会更新数据。- 如果不满足
l >= 0就进入下一次循环,不更新数据。
- 如果不满足
- 更新数据:如果第 2 步的判断为
true,那就把当前ans和now中的较大值赋给ans。这样到最后ans就是子数组和的最大值。 - 退出窗口:
now -= nums[l]。
上面四步是定长滑动窗口的模板解法,适用于每一个定长滑动窗口问题。通常来说,最困难的部分就是寻找窗口大小和起始点。因为窗口不仅能从左往右滑,也可以从右往左滑。通过合适地确定 r 值能将这两种情况合并到同一个循环中。
时间复杂度:
O(n)。右端点需要访问每一个元素。空间复杂度:通常为
O(1),但如果需要用哈希表等记录窗口内元素信息,则可能为O(k)或O(字符集大小)1。
那么接下来就看一些寻找符合条件窗口的问题。
子数组 - 数组内元素唯一
现在我们给窗口增加一个限制:子数组必须保证有若干个元素互不相同。
这可以用 Go 中的映射(map)来记录元素出现次数。像这样,在一个数据类型中,一个值对应另一个值的,我们叫它哈希表(Hashmap)。下同。
freq := map[int]int{}上面就是一个统计字符出现顺序的哈希表。我们可以使用 freq[num]++ 和 freq[num]-- 来修改元素出现顺序。
以 2841. 几乎唯一子数组的最大和 - 力扣(LeetCode)和为例。我们至少需要让 len(freq) >= m 才更新 ans。2461. 长度为 K 子数组中的最大和 - 力扣(LeetCode) 则只需要让 len(freq) == k 即可。
给你一个整数数组
nums和两个正整数m和k。请你返回
nums中长度为k的 几乎唯一 子数组的 最大和 ,如果不存在几乎唯一子数组,请你返回0。如果
nums的一个子数组有至少m个互不相同的元素,我们称它是 几乎唯一 子数组。子数组指的是一个数组中一段连续 非空 的元素序列。
在这里,每当右端点进入窗口时,就需要 freq[nums[r]]++;左端点出窗口时,则需要 freq[nums[l]]-- 并且注意删到 0 就要清空哈希表中的这一项。(因为我们实际用到的是哈希表的长度)
func maxSum(nums []int, m int, k int) int64 {
var ans, now int
freq := map[int]int{} // 统计字符出现次数
for r := range nums {
now += nums[r]
freq[nums[r]]++
l := r-k+1
if l < 0 {
continue
}
if len(freq) >= m {
ans = max(ans, now)
}
// 如果是 leco2641
/*
if len(freq) == k {
ans = max(ans, now)
}
*/
now -= nums[l]
freq[nums[l]]--
if freq[nums[l]] == 0 {
delete(freq, nums[l])
}
}
return int64(ans)
}子数组 - 窗口有破洞
现在的走廊上有无法照亮的地方,即使我们用探照灯,也什么都看不见。但是幸运的是,我们不需要考虑破洞的元素是否需要加入窗口里,因为无论如何答案里都会加上破洞(无需考虑的元素)的值。
我们看看怎样把这部分破洞正确处理。
有一个书店老板,他的书店开了
n分钟。每分钟都有一些顾客进入这家商店。给定一个长度为n的整数数组customers,其中customers[i]是在第i分钟开始时进入商店的顾客数量,所有这些顾客在第i分钟结束后离开。在某些分钟内,书店老板会生气。 如果书店老板在第
i分钟生气,那么grumpy[i] = 1,否则grumpy[i] = 0。当书店老板生气时,那一分钟的顾客就会不满意,若老板不生气则顾客是满意的。
书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续
minutes分钟不生气,但却只能使用一次。请你返回 这一天营业下来,最多有多少客户能够感到满意 。
我们总结一下题目,能够得到这样的事实。
minutes是窗口长度。grumpy[i] == 1则应该将customers[i]加入窗口。grumpy[i] == 0则应该忽略customers[i]。- 无论
grumpy[i]是多少,customers[i]都会占用窗口长度。- 也就是说窗口内满足
grumpy[i] == 0的customers[i]可视作0。
- 也就是说窗口内满足
我们可以使用一个数组 sat 来记录,sat[0] 表示老板不生气时的顾客数目,sat[1] 表示老板生气但是抑制住情绪(即仍然满意)的顾客数。
接着用条件控制 customers[i] 的进出窗口,如下所示。
var sat = [2]int{}
if grumpy[r] == 1 {
now += customers[r]
} else {
sat[grumpy[i]] += customers[r]
}
// ...
if grumpy[l] == 1 {
now -= customers[l]
}知道了怎么处理破洞的窗口,那就很好写出完整的实现代码了。
func maxSatisfied(customers []int, grumpy []int, minutes int) int {
var sat = [2]int{} // 最多满意的顾客数
var now int // 老板愤怒时的顾客数(窗口长度为 minutes)
for r, c := range customers {
// 下面的 if else 用来分流老板状态不同时的顾客数
if grumpy[r] == 1 {
now += c
} else {
sat[grumpy[r]] += c
}
l := r - minutes + 1
if l < 0 {
continue
}
sat[1] = max(now, sat[1]) // 更新最多的老板愤怒时的顾客数
if grumpy[l] == 1 {
now -= customers[l]
}
}
return sat[0] + sat[1]
}自己挖破洞 - 抛弃元素问题
我们把上面的数组内元素唯一和窗口有破洞结合起来。我们此时需要保证窗口内有不超过 m 个相同的元素,多了要扔掉。
扔掉的元素不再计入窗口内元素之和,但是仍然占用窗口长度。
这就是 leco3679。
给你两个整数 w 和 m,以及一个整数数组 arrivals,其中 arrivals[i] 表示第 i 天到达的物品类型(天数从 1 开始编号)。
物品的管理遵循以下规则:
- 每个到达的物品可以被 保留 或 丢弃 ,物品只能在到达当天被丢弃。
- 对于每一天
i,考虑天数范围为[max(1, i - w + 1), i](也就是直到第i天为止最近的w天):
- 对于 任何 这样的时间窗口,在被保留的到达物品中,每种类型最多只能出现
m次。- 如果在第
i天保留该到达物品会导致其类型在该窗口中出现次数 超过m次,那么该物品必须被丢弃。返回为满足每个
w天的窗口中每种类型最多出现m次,最少 需要丢弃的物品数量。
只要用哈希表记录元素出现次数,并且在抛弃元素后把被抛弃的元素设置为 0 即可。这是因为原题中的数据范围决定了 arrivals[i] >= 1,如果有 0 就不能这样做。
剩下的部分与常规滑动窗口完全一致。
func minArrivalsToDiscard(arrivals []int, w int, m int) int {
var freq = map[int]int{} // 记录元素出现次数
var ans int
for r := range arrivals {
freq[arrivals[r]]++
if freq[arrivals[r]] > m {
ans++
freq[arrivals[r]]--
// 易错点!否则出窗口时会导致已经抛弃的元素再抛弃一次
arrivals[r] = 0
}
l := r - w + 1
if l < 0 {
continue
}
freq[arrivals[l]]--
}
return ans
}寻找窗口
窗口初始位置不同 - 循环数组
循环数组的意思是,一个数组的最后一项的下一项恰好是第一项,这就意味着这个数组对于任何大于等于零的索引2都不会 panic。
一个循环数组的第 i 位索引可以表示为 nums[i%len(nums)]。
在这样的数组里,窗口端点索引可以大于等于数组长度,因此滑动窗口既可以从右向左滑,也可以从左向右滑。但是!通过合理地选择窗口起点,完全能把这两种情况合并到一起。
leco1652 拆炸弹 就是这样的一道题。
你有一个炸弹需要拆除,时间紧迫!你的情报员会给你一个长度为
n的 循环 数组code以及一个密钥k。为了获得正确的密码,你需要替换掉每一个数字。所有数字会 同时 被替换。(注:这一句可以忽略)
- 如果
k > 0,将第i个数字用 接下来k个数字之和替换。- 如果
k < 0,将第i个数字用 之前k个数字之和替换。- 如果
k == 0,将第i个数字用0替换。由于
code是循环的,code[n-1]下一个元素是code[0],且code[0]前一个元素是code[n-1]。给你 循环 数组
code和整数密钥k,请你返回解密后的结果来拆除炸弹!
先观察一下窗口运行的特点。设解密后的数组为 ans。
k > 0:ans[0]填入的就是code[1 : k+1]求和的值。k < 0:ans[0]填入的就是code[n+k : n]求和的值。
将这个结论推广下去。(省略循环数组的取余操作)
k > 0:ans[i]填入的就是code[i+1 : k+i+1]求和的值。k < 0:ans[i]填入的就是code[n+k+i : n+i]求和的值。
把窗口的起始点搞明白之后,先写初始化窗口的代码。
n := len(code)
r := k + 1
// 然后 k < 0
if k < 0 {
r = n
k = -k
}上面的代码完全仿照了一开始的推导,那么接下来就写滑动窗口部分。
// 把第一个窗口内的和计算出来
var now int
for _, c := range code[r-k : r] {
now += c
}
// 窗口开始滑动
var ans = make([]int, n)
for i := range code {
ans[i] = now
// 在第一个窗口的基础上开始滑动
now += code[r%n] - code[(r-k)%n] // 因为循环数组,所以要取余运算
// 这里的 r-k 就是左端点
r++
}
return ans也就是这样。
func decrypt(code []int, k int) []int {
// 先写 k > 0 的情况
n := len(code)
r := k + 1
// 然后 k < 0
if k < 0 {
r = n
k = -k
}
// 把第一个窗口内的和计算出来
var now int
for _, c := range code[r-k : r] {
now += c
}
// 窗口开始滑动
var ans = make([]int, n)
for i := range code {
ans[i] = now
now += code[r%n] - code[(r-k)%n] // 因为循环数组,所以要取余运算
// 这里的 r-k 就是左端点
r++
}
return ans
}这就是拆炸弹的解法。这里不需要特判 k == 0 的情况。因为此时的 r 与 r-k 是同一个数,滑动时会互相抵消。
寻找窗口 - 重新安排活动时间
3439. 重新安排会议得到最多空余时间 I - 力扣(LeetCode)
给你一个整数
eventTime表示一个活动的总时长,这个活动开始于t = 0,结束于t = eventTime。同时给你两个长度为
n的整数数组startTime和endTime。它们表示这次活动中n个时间 没有重叠 的会议,其中第i个会议的时间为[startTime[i], endTime[i]]。你可以重新安排 至多
k个会议,安排的规则是将会议时间平移,且保持原来的 会议时长 ,你的目的是移动会议后 最大化 相邻两个会议之间的 最长 连续空余时间。移动前后所有会议之间的 相对 顺序需要保持不变,而且会议时间也需要保持互不重叠。
请你返回重新安排会议以后,可以得到的 最大 空余时间。
注意,会议 不能 安排到整个活动的时间以外。
我们观察一下活动时间与空余时间的关系。
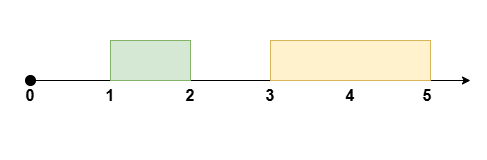
容易发现,每一段活动时间的左侧都有一段对应的空余时间,而在最后又有一段空余时间(空余时长为 0 也计入)。
这也就意味着,设原题给出的 startTime 长度为 n,空余时间的段数就是 n+1。
我们把空余时间抽象成一个数组 free,其中 free[i] 表示第 i 段空余时间的长度(可以是 0)。
然后我们发现,每操作一段会议时间,实际上是合并了两段空余时间。
推广下去,操作 k 段会议时间就是合并了 k+1 段空余时间。**而且!**这 k+1 段空余时间在 free 数组中是连续的。
有没有觉得很熟悉?没错,问题就转化成了在 free 数组中寻找长为 k+1 的子数组,并保证子数组内元素和最大。
这又是一道经典的定长滑动窗口,直接套入模板。但在开始前需要写一个生成 free 数组的代码。
func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {
// 生成 free 数组
n := len(startTime)
free := make([]int, n+1)
free[0] = startTime[0]
for i := 1; i < n; i++ {
free[i] = startTime[i] - endTime[i-1]
}
free[n] = eventTime - endTime[n-1]
// 开始滑动窗口
var now, ans int
for r := range free {
now += free[r]
l := r - k
if l < 0 {
continue
}
ans = max(now, ans)
now -= free[l]
}
return ans
}滑动窗口 - 长度不固定
当窗口长度不定时,此时我们不能再用上面的 进-判-出 三步走,这时候进出窗口完全靠我们自行判断了。
先用一道模板题试试水。
3. 无重复字符的最长子串 - 力扣(LeetCode) 这道题还有一个兄弟版本 leco3090。
给一个字符串
s,请你找出其中不含有重复字符的 最长 子串 的长度。子串是字符串中连续的非空字符序列。
这可用下面的流程表示。
- 右端点进入窗口
- 判断现在进入窗口的字符是否已经出现超过
1次。true收缩左窗口直到当前字符出现次数等于1。false不做处理,继续。
- 用一个变量
ans在每次循环末尾存储当前ans与r-l+1中的较大值。
上面流程清晰易懂,所以直接展示代码。
func lengthOfLongestSubstring(s string) int {
var freq = map[byte]int{}
var l, ans int
for r := range s {
freq[s[r]]++ // 右端点进入窗口
for freq[s[r]] > 1 { // 左端点离开窗口的条件
freq[s[l]]--
l++
}
ans = max(ans, r-l+1) // 取较大值
}
return ans
}可视化:
将要操作的字符串: abcabcbb
当前窗口: a
当前窗口: ab
当前窗口: abc
当前窗口: abca
⚠️ 发现重复字符 'a' 窗口收缩
当前窗口: bca
当前窗口: bcab
⚠️ 发现重复字符 'b' 窗口收缩
当前窗口: cab
当前窗口: cabc
⚠️ 发现重复字符 'c' 窗口收缩
当前窗口: abc
当前窗口: abcb
⚠️ 发现重复字符 'a' 窗口收缩
当前窗口: bcb
⚠️ 发现重复字符 'b' 窗口收缩
当前窗口: cb
当前窗口: cbb
⚠️ 发现重复字符 'c' 窗口收缩
当前窗口: bb
⚠️ 发现重复字符 'b' 窗口收缩
当前窗口: b
最终答案: 3不定长窗口 - 反向窗口
所谓反向窗口,就是我们实际求得的窗口是恰好与答案相反的。
我们这里会提到一个非常重要的思想:正难则反。
顾名思义,如果我们正向求解一个问题是困难的,那不妨从答案的对立事件入手,然后用全集减去对立事件,这样可能会方便一点。
例如抽卡问题:1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode)
注:这里把数组看作一排卡片,每个元素就是一张卡片。
给你一个整数数组
nums和一个整数x。每一次操作时,你应当移除数组nums最左边或最右边的元素,然后从x中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。如果可以将
x恰好 减到0,返回 最小操作数 ;否则,返回-1。
如果我们真的从左边和右边开始,一张一张抽卡试探,那是很麻烦的。
那我们换个思路,看看抽完卡之后剩下的卡片有什么特点。
设 nums 全部元素求和的值是 s,那么如果能够让 x == 0,抽完之后的卡片求和就是 s-x (设为 target)。
那我们就可以在这排卡片中寻找最长的一段,让这一段的卡片数字之和等于 target。
有没有发现这就是越长越好的不定长滑动窗口?那我们就用模板代码写出来。
func minOperations(nums []int, x int) int {
var now, l int
var ans int = -1 // 默认找不到 x
var target int = -x
for _, i := range nums {
target += i // 这样求出来就是上面所说的 s-x
}
if target < 0 {
// 此时的 x 大于 nums 所有元素之和
// 找不到,直接返回
return ans
}
// 下面就是模板代码
for r := range nums {
now += nums[r]
for now > target {
now -= nums[l]
l++
}
if now == target { // 只有在 now == s-x 才更新
ans = max(ans, r-l+1)
}
}
if ans < 0 {
return -1
}
return len(nums) - ans
}不定长窗口 - 越短越好
这里的越短越好指的是窗口覆盖所有所需元素时,窗口越短越好。
这大多出现在寻找最短子串问题中,例如 76. 最小覆盖子串 - 力扣(LeetCode)。
给你一个字符串
s、一个字符串t。返回s中涵盖t所有字符的最小子串。如果s中不存在涵盖t所有字符的子串,则返回空字符串""。注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。- 如果
s中存在这样的子串,我们保证它是唯一的答案。
这还是道困难题,解开你的困难题解答数就 +1 了。
因为 s 和 t 中只有英文字母,所以考虑用长为 123 (比 z 对应的 ASCII 码点 122 多 1。因为索引从 0 开始,所以这样能方便运算)的数组 freq 来标记 t 与 s 中存储的字符。
然后用一个变量 types 来记录 t 字符种类数,每当检测到 freq[i] == 0 时 types--,这样就能够做到同时统计字符数和字符种类。
当 types == 0 时,意味着已经搜索到了一个含有 t 中全部字符的子串,就考虑收缩窗口寻找更优解。
func minWindow(s string, t string) string {
var freq = [123]int{}
var types int // t 的字符种类数
for i := range t {
if freq[t[i]] == 0 { // 新的字符种类
types++
}
freq[t[i]]++
}
var l int
ansl, ansr := -1, 2147483647 // 大到不可能的边界
for r := range s {
freq[s[r]]--
if freq[s[r]] == 0 { // 窗口中 s[r] 这个字符的数量,刚好满足了 t 的要求,不多也不少
types--
}
// 找到了 t 中所有的字符(数目也一致)
for types == 0 {
if r-l < ansr-ansl { // 更新答案
ansl, ansr = l, r
}
// 在把 s[l] 移出窗口之前,s[l] 是一个数量刚刚好的关键字符
// 也就是说,这时候还将 freq[s[l]] 移出,就不满足要求了
if freq[s[l]] == 0 {
types++
}
freq[s[l]]++
l++ // 边界收缩
}
}
if ansl == -1 { // 特判未找到的情况
return ""
}
return s[ansl : ansr+1]
}把搜索过程可视化,就是这样的。
输入:
s := "ADOBECODEBANC"
t := "ABC"
t 包含的字符种类数: 3
==================================
搜索进度: 1 / 13
当前子串包含的字符种类数: 1
当前扫描得到的子串: "A"
==================================
搜索进度: 2 / 13
当前子串包含的字符种类数: 1
当前扫描得到的子串: "AD"
==================================
搜索进度: 3 / 13
当前子串包含的字符种类数: 1
当前扫描得到的子串: "ADO"
==================================
搜索进度: 4 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "ADOB"
==================================
搜索进度: 5 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "ADOBE"
==================================
搜索进度: 6 / 13
当前子串包含的字符种类数: 3
当前扫描得到的子串: "ADOBEC"
满足条件!将尝试收缩窗口。当前子串:"ADOBEC"
==================================
搜索进度: 7 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "DOBECO"
==================================
搜索进度: 8 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "DOBECOD"
==================================
搜索进度: 9 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "DOBECODE"
==================================
搜索进度: 10 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "DOBECODEB"
==================================
搜索进度: 11 / 13
当前子串包含的字符种类数: 3
当前扫描得到的子串: "DOBECODEBA"
满足条件!将尝试收缩窗口。当前子串:"DOBECODEBA"
满足条件!将尝试收缩窗口。当前子串:"OBECODEBA"
满足条件!将尝试收缩窗口。当前子串:"BECODEBA"
满足条件!将尝试收缩窗口。当前子串:"ECODEBA"
满足条件!将尝试收缩窗口。当前子串:"CODEBA"
==================================
搜索进度: 12 / 13
当前子串包含的字符种类数: 2
当前扫描得到的子串: "ODEBAN"
==================================
搜索进度: 13 / 13
当前子串包含的字符种类数: 3
当前扫描得到的子串: "ODEBANC"
满足条件!将尝试收缩窗口。当前子串:"ODEBANC"
满足条件!将尝试收缩窗口。当前子串:"DEBANC"
满足条件!将尝试收缩窗口。当前子串:"EBANC"
满足条件!将尝试收缩窗口。当前子串:"BANC"
最终答案: "BANC"额外部分
其实定长滑动窗口还可以优化,例如 leco634 子数组最大平均数 I 可以这样写。
func findMaxAverage(nums []int, k int) float64 {
var now int
// 计算第一个窗口和
for _, x := range nums[:k] {
now += nums[r]
}
for r := k; r < len(nums); r++ {
now += nums[r] - nums[r-k]
ans = max(ans, now) // 取最大值
}
return float64(ans) / float64(k)
}这种优化思路就是,先计算第一个窗口值,然后把第一个窗口值作为 ans 的初始值,然后从 k 处开始遍历寻找窗口。
在这之后只要将 now += nums[r] - nums[r-k] 就能实现更新窗口值。
因为写了一篇困难题的解决思路,就把它作为双指针和滑动窗口的第二部分结尾吧,第三部分讲一些特殊的窗口。
滑动窗口实际上是在维护一个队列(queue),队列遵循先进先出(First In First Out, FIFO)的原则。
这个队列最多只会遍历整个数组或字符串一次,因此单纯滑动窗口算法的时间复杂度只有 O(n),比暴力搜索高效得多。
队列有一个头和一个尾,头就是窗口的左端点,尾就是窗口的右端点。元素不断地从右端点进入窗口,又不断地从左端点离开窗口,这就对应了队列的“入队”(enqueue)和“出队”(dequeue)操作。
这就是滑动窗口的本质。因为队列在原序列中必然连续,因此滑动窗口极其适合解决子数组/子串问题,并能把至少
O(n^2)的暴力搜索优化到O(n)。
这是 双指针与滑动窗口 的第二部分,在这里,我们接触了定长滑动窗口的模板,并且看了一些窗口长度藏得极其诡异的题目。
然后给下一期的不定长滑动窗口起了一个头。因为滑动窗口本质是在维护一个队列。
这个队列当条件满足时入队,条件不满足时出队。
本期教程就到这里,下一期(第三部分)就涉及一些特别的窗口问题。
🎉撒花!🎉